Genetic Algorithms Belong to the Family of Methods in the

Genetic Algorithms(GAs) are adaptive heuristic search algorithms that vest to the larger part of evolutionary algorithms. Genetic algorithms are based on the ideas of natural choice and genetics. These are intelligent exploitation of random search provided with historical data to direct the search into the region of ameliorate functioning in solution space. They are normally used to generate high-quality solutions for optimization issues and search problems.

Genetic algorithms simulate the process of natural selection which means those species who can adapt to changes in their environment are able to survive and reproduce and become to next generation. In simple words, they simulate "survival of the fittest" among private of consecutive generation for solving a trouble. Each generation consist of a population of individuals and each private represents a point in search space and possible solution. Each individual is represented as a string of character/integer/float/bits. This cord is analogous to the Chromosome.

Foundation of Genetic Algorithms

Genetic algorithms are based on an analogy with genetic structure and behavior of chromosomes of the population. Following is the foundation of GAs based on this analogy –

1. Private in population compete for resources and mate
2. Those individuals who are successful (fittest) and so mate to create more than offspring than others
3. Genes from "fittest" parent propagate throughout the generation, that is sometimes parents create offspring which is better than either parent.
4. Thus each successive generation is more suited for their surround.

Search space

The population of individuals are maintained inside search space. Each individual represents a solution in search space for given trouble. Each individual is coded as a finite length vector (analogous to chromosome) of components. These variable components are analogous to Genes. Thus a chromosome (individual) is composed of several genes (variable components).

Fitness Score

A Fettle Score is given to each individual which shows the ability of an private to "compete". The private having optimal fettle score (or almost optimal) are sought.

The GAs maintains the population of northward individuals (chromosome/solutions) forth with their fitness scores.The individuals having better fitness scores are given more chance to reproduce than others. The individuals with better fitness scores are selected who mate and produce better offspring by combining chromosomes of parents. The population size is static and then the room has to be created for new arrivals. So, some individuals die and go replaced by new arrivals eventually creating new generation when all the mating opportunity of the old population is exhausted. It is hoped that over successive generations amend solutions will go far while least fit die.

Each new generation has on boilerplate more "better genes" than the private (solution) of previous generations. Thus each new generations have better "partial solutions" than previous generations. Once the offspring produced having no meaning difference from offspring produced by previous populations, the population is converged. The algorithm is said to be converged to a set up of solutions for the problem.

Operators of Genetic Algorithms

Once the initial generation is created, the algorithm evolves the generation using post-obit operators –
1) Selection Operator: The idea is to requite preference to the individuals with good fitness scores and let them to laissez passer their genes to successive generations.
2) Crossover Operator: This represents mating between individuals. Two individuals are selected using selection operator and crossover sites are called randomly. And then the genes at these crossover sites are exchanged thus creating a completely new private (offspring). For example –

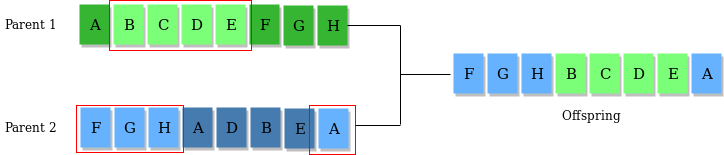
3) Mutation Operator: The primal idea is to insert random genes in offspring to maintain the diversity in the population to avoid premature convergence. For example –

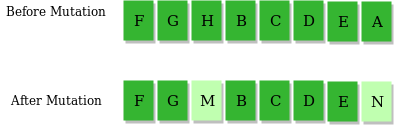
The whole algorithm can be summarized every bit –

ane) Randomly initialize populations p 2) Determine fitness of population iii) Until convergence echo:       a) Select parents from population       b) Crossover and generate new population       c) Perform mutation on new population       d) Calculate fitness for new population

Instance problem and solution using Genetic Algorithms

Given a target cord, the goal is to produce target string starting from a random string of the same length. In the following implementation, post-obit analogies are made –

• Characters A-Z, a-z, 0-9, and other special symbols are considered as genes
• A string generated by these characters is considered every bit chromosome/solution/Individual

Fettle score is the number of characters which differ from characters in target string at a particular index. Then individual having lower fitness value is given more preference.

C++

#include <bits/stdc++.h>

using namespace std;

#define POPULATION_SIZE 100

const string GENES = "abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOP" \

"QRSTUVWXYZ 1234567890, .-;:_!\"#%&/()=?@${[]}" ;

const cord TARGET = "I love GeeksforGeeks" ;

int random_num( int start, int cease)

{

int range = (end-start)+1;

int random_int = start+( rand ()%range);

render random_int;

}

char mutated_genes()

{

int len = GENES.size();

int r = random_num(0, len-1);

render GENES[r];

}

string create_gnome()

{

int len = TARGET.size();

cord gnome = "" ;

for ( int i = 0;i<len;i++)

gnome += mutated_genes();

return gnome;

}

class Individual

{

public :

string chromosome;

int fitness;

Individual(cord chromosome);

Individual mate(Individual parent2);

int cal_fitness();

};

Individual::Private(cord chromosome)

{

this ->chromosome = chromosome;

fitness = cal_fitness();

};

Individual Individual::mate(Private par2)

{

string child_chromosome = "" ;

int len = chromosome.size();

for ( int i = 0;i<len;i++)

{

bladder p = random_num(0, 100)/100;

if (p < 0.45)

child_chromosome += chromosome[i];

else if (p < 0.90)

child_chromosome += par2.chromosome[i];

else

child_chromosome += mutated_genes();

}

return Individual(child_chromosome);

};

int Individual::cal_fitness()

{

int len = TARGET.size();

int fitness = 0;

for ( int i = 0;i<len;i++)

{

if (chromosome[i] != TARGET[i])

fitness++;

}

return fitness;

};

bool operator<( const Private &ind1, const Individual &ind2)

{

render ind1.fitness < ind2.fitness;

}

int main()

{

strand((unsigned)( time (0)));

int generation = 0;

vector<Individual> population;

bool establish = false ;

for ( int i = 0;i<POPULATION_SIZE;i++)

{

string gnome = create_gnome();

population.push_back(Individual(gnome));

}

while (! found)

{

sort(population.begin(), population.stop());

if (population[0].fitness <= 0)

{

found = true ;

intermission ;

}

vector<Individual> new_generation;

int southward = (ten*POPULATION_SIZE)/100;

for ( int i = 0;i<south;i++)

new_generation.push_back(population[i]);

s = (90*POPULATION_SIZE)/100;

for ( int i = 0;i<s;i++)

{

int len = population.size();

int r = random_num(0, l);

Individual parent1 = population[r];

r = random_num(0, l);

Private parent2 = population[r];

Private offspring = parent1.mate(parent2);

new_generation.push_back(offspring);

}

population = new_generation;

cout<< "Generation: " << generation << "\t" ;

cout<< "Cord: " << population[0].chromosome << "\t" ;

cout<< "Fitness: " << population[0].fitness << "\n" ;

generation++;

}

cout<< "Generation: " << generation << "\t" ;

cout<< "Cord: " << population[0].chromosome << "\t" ;

cout<< "Fitness: " << population[0].fitness << "\n" ;

}

Python3

import random

POPULATION_SIZE = 100

GENES =

TARGET = "I love GeeksforGeeks"

class Individual( object ):

def __init__( self , chromosome):

self .chromosome = chromosome

cocky .fettle = self .cal_fitness()

@classmethod

def mutated_genes( cocky ):

global GENES

gene = random.pick(GENES)

return gene

@classmethod

def create_gnome( cocky ):

global TARGET

gnome_len = len (TARGET)

return [ self .mutated_genes() for _ in range (gnome_len)]

def mate( self , par2):

child_chromosome = []

for gp1, gp2 in cipher ( self .chromosome, par2.chromosome):

prob = random.random()

if prob < 0.45 :

child_chromosome.append(gp1)

elif prob < 0.90 :

child_chromosome.append(gp2)

else :

child_chromosome.append( self .mutated_genes())

return Individual(child_chromosome)

def cal_fitness( self ):

global TARGET

fitness = 0

for gs, gt in aught ( self .chromosome, TARGET):

if gs ! = gt: fettle + = ane

return fitness

def primary():

global POPULATION_SIZE

generation = one

constitute = Imitation

population = []

for _ in range (POPULATION_SIZE):

gnome = Individual.create_gnome()

population.append(Individual(gnome))

while not constitute:

population = sorted (population, primal = lambda x:10.fitness)

if population[ 0 ].fettle < = 0 :

found = True

suspension

new_generation = []

s = int (( 10 * POPULATION_SIZE) / 100 )

new_generation.extend(population[:southward])

s = int (( ninety * POPULATION_SIZE) / 100 )

for _ in range (southward):

parent1 = random.pick(population[: 50 ])

parent2 = random.choice(population[: 50 ])

child = parent1.mate(parent2)

new_generation.append(child)

population = new_generation

impress ( "Generation: {}\tString: {}\tFitness: {}" .\

format (generation,

"".join(population[ 0 ].chromosome),

population[ 0 ].fitness))

generation + = 1

impress ( "Generation: {}\tString: {}\tFitness: {}" .\

format (generation,

"".join(population[ 0 ].chromosome),

population[ 0 ].fitness))

if __name__ = = '__main__' :

primary()

Output:

Generation: ane    String: tO{"-?=jH[k8=B4]Oe@}    Fitness: xviii Generation: 2    Cord: tO{"-?=jH[k8=B4]Oe@}    Fettle: 18 Generation: 3    String: .#lRWf9k_Ifslw #O$k_    Fitness: 17 Generation: 4    String: .-1Rq?9mHqk3Wo]3rek_    Fettle: sixteen Generation: 5    Cord: .-1Rq?9mHqk3Wo]3rek_    Fitness: xvi Generation: half-dozen    String: A#ldW) #lIkslw cVek)    Fettle: xiv Generation: 7    String: A#ldW) #lIkslw cVek)    Fitness: xiv Generation: 8    String: (, o 10 _x%Rs=, 6Peek3   Fettle: 13                            .                             .                             .  Generation: 29    String: I lope Geeks#o, Geeks   Fitness: 3 Generation: thirty    String: I loMe GeeksfoBGeeks    Fettle: two Generation: 31    String: I love Geeksfo0Geeks    Fitness: 1 Generation: 32    String: I love Geeksfo0Geeks    Fitness: 1 Generation: 33    String: I dear Geeksfo0Geeks    Fitness: 1 Generation: 34    String: I love GeeksforGeeks    Fitness: 0

Annotation: Everytime algorithm start with random strings, so output may differ

As we can run across from the output, our algorithm sometimes stuck at a local optimum solution, this can be further improved by updating fitness score adding algorithm or past tweaking mutation and crossover operators.

Why use Genetic Algorithms

• They are Robust
• Provide optimisation over large space state.
• Unlike traditional AI, they practise not interruption on slight modify in input or presence of noise

Awarding of Genetic Algorithms

Genetic algorithms have many applications, some of them are –

• Recurrent Neural Network
• Mutation testing
• Code breaking
• Filtering and point processing
• Learning fuzzy rule base of operations etc

References
https://en.wikipedia.org/wiki/List_of_genetic_algorithm_applications
https://en.wikipedia.org/wiki/Genetic_algorithm
https://www.md.ic.ac.uk/~nd/surprise_96/journal/vol1/hmw/article1.html
This article is contributed by Atul Kumar. If you like GeeksforGeeks and would like to contribute, you lot can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. Meet your article actualization on the GeeksforGeeks main page and help other Geeks.
Please write comments if you lot discover anything incorrect, or you want to share more information about the topic discussed higher up.

ogleshitery.blogspot.com

Source: https://www.geeksforgeeks.org/genetic-algorithms/

Share this post